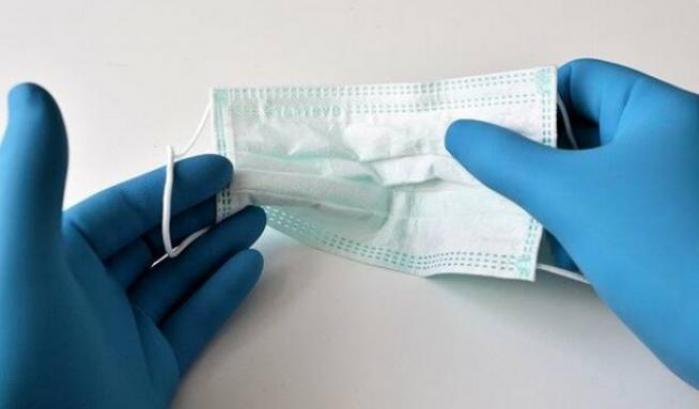
Un team di ricercatori della scuola di ingegneria della Johns Hopkins presenta, in un nuovo studio pubblicato su Physics of Fluids, una formula per comprendere e calcolare con maggior dettaglio le possibilità che il virus SARS-CoV-2 possa trasmettersi per via aerea da una persona ad un’altra.
L’equazione ricalca quella dell’astronomo Frank Drake che fu sviluppata per calcolare la probabilità di trovare una civiltà extraterrestre intelligente nella via Lattea. La cosiddetta legge di Drake ha sempre diviso la comunità scientifica perché troppo piena di variabili obiettivamente sconosciute.
La formula messa in campo nella ricerca, denominata “disuguaglianza di trasmissione aerea del contagio”, presenta una previsione del rischio che comunque può variare notevolmente a seconda dello scenario ma cerca di analizzare attraverso un calcolo statistico e matematico l’importanza delle mascherine e del distanziamento. I ricercatori hanno, ad esempio, calcolato che se due persone indossano entrambe maschere N95, il rischio di trasmissione del virus da una persona all’altra viene ridotto di un fattore 400. In pratica esiste meno dell’1% di possibilità di contrarre in questo caso il virus.
Anche le mascherine semplici, quelle fatte in tessuto o le più classiche “mascherine chirurgiche”, comunque, secondo la formula, tendono a ridurre significativamente le probabilità di trasmissione.